尾崎スキームを知っているか？いずれわかる

Doug Eadline　　オリジナル記事「Have You Heard About the Ozaki Scheme? You Will」

HPCにおけるアクセラレーターの使用は、パフォーマンスを新たなレベルに押し上げた。初期のGPUに始まり、（SIMD処理の形で）並列処理ハードウェアを活用する能力は、HPC性能に大きな恩恵をもたらした。その結果、FortranやC言語向けのツールセットはもちろんのこと、ECCメモリや高速64ビット倍精度などの機能を含むGPU設計にとって、HPC市場は大きな推進力となってきた。

その関係が変わりつつある。AIの成長と、低解像度コンピューティングをサポートするハードウェアへの需要が、GPU設計に再び焦点を当てている。例えば、多くのHPCユーザは、エヌビディアGPUに搭載されているCUDAコアに慣れ親しんでいる。これらのプロセッシング・ユニットはシーケンシャル処理に優れており、シミュレーションや汎用GPUグラフィックス・コンピューティングのHPCアプリケーションに（膨大な数で）使用されている。CUDAコアはFP32およびFP64レベルの精度を持ち、CUDAプログラミング・モデルを使ってプログラムすることができる。

2017年、エヌビディアはVoltaアーキテクチャにTensorコアを導入した。CUDAコアとは異なり、テンソルコアは低精度の行列乗算と畳み込み演算用に設計されており、浮動小数点（FP16、FP32）と整数（INT8、INT4）の両方をサポートしている。

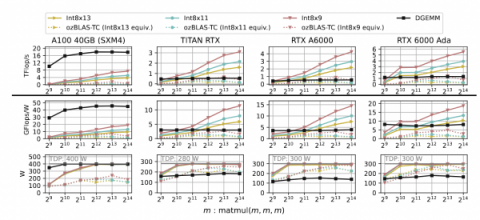
例えば、エヌビディアB200 GPUは、16,896個のCUDAコアと528個のテンソル・コアを搭載している。下図に示すように、テンソルコア（TCで表記）のFLOPS/TOPS性能は向上しており、精度が低いためCUDAコア（FP32とFP64）よりもはるかに高い。

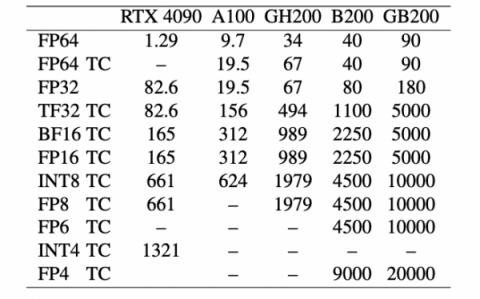表は、「Performance Enhancement of Ozaki Scheme on Integer Matrix Multiplication Unit」(https://arxiv.org/pdf/2409.13313) による。

GPU（エヌビディアとAMDの両方）上のAI領域と低精度AI性能の成長は間違いなく続くだろう。HPCコミュニティにとって幸運なことに、高性能なAI機能（テンソル・コア）をエヌビディアで使用し、HPCアプリケーションに必要な精度を実現する方法が開発されている。

テンソル・コアがエヌビディアGPUに搭載される5年前の2012年、尾崎勝久、荻田剛、大石慎一、ジークフリート・M・ランプは、「Error-free transformations of matrix multiplication by using fast routines of matrix multiplication and its applications 」と題する論文を発表した。 この論文の中で著者らは、浮動小数点数のエラーのない高速分割の技法について述べている。この技法を用いて、著者らはまず、2つの浮動小数点行列の積を浮動小数点行列の和に変換するエラーのない変換を開発した。

尾崎スキームとは、低精度計算を活用して高精度の行列乗算を行う方法である。これは、高精度の入力行列を複数の成分に分割し、これらの成分に対して低精度演算を用いて行列乗算を行うことで実現される。その結果を組み合わせて、最終的な高精度行列積を得る。

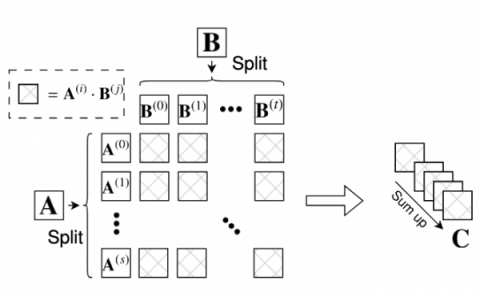低精度演算ユニットでの高精度行列乗算C ← A – Bアルゴリズムの基本計算

このスキームが、低精度行列を使用しながら精度を維持できることを実証したことで、低精度テンソルコアを高精度HPC浮動小数点に適応させる道が開かれた。スキームは以下のように機能する：

1. 分割： 高精度入力行列を複数の低精度コンポーネントまたはスライスに分割する。
2. 低精度乗算： 各成分は、GPU（テンソル・コア）のような特殊なハードウェアで効率的に実装できる低精度演算を使用して乗算される。
3. 累積： 低精度乗算の結果は高精度で累積される。
4. 精度： この方式は、計算の一部に低精度演算を使用しても、従来の高精度行列乗算と同じ精度を達成できる。

尾崎スキームは高性能であることも示されている。あるプラットフォームでは、（CUDAコアを使った）ネイティブ高精度演算の性能を上回る場合もある。さらに、（テンソルコアだけでなく）さまざまなデータ型やハードウェアで使用されており、さまざまな行列乗算タスクに対する汎用性の高いアプローチとなっている。

低精度の計算ユニットで高精度の行列乗算を計算することに加え、尾崎スキームには3つの利点がある：

1. 尾崎スキームは、FP64よりもさらに高精度の可変精度で計算できる。尾崎スキームの精度は、分割数と部分行列の合計処理の精度を変えることで調整できる。興味深いことに、分割数を調整することで、IEEE標準精度の中間精度、すなわちFP32とFP64の中間精度で行列の乗算を行うことができ、所望の／要求される精度レベルを維持しながら性能を向上させることができる。
2. 浮動小数点演算の回数が少なくて済むため、丸め誤差は標準浮動小数点パッケージで計算されたGEMM（General Matrix Multiply）結果よりも小さくなる。
3. この方式は、高度に最適化されたBLAS（Basic Linear Algebra Subprograms）パッケージによって実装することができる。インテルMKLやエヌビディアcuBLASのようなプロセッサに最適化されたライブラリと同様に、尾崎スキームも実装できる。

しかし、尾崎方式には主に2つの欠点がある：

1. 行列のスライスを保存するために大量のワーキングメモリーを必要とする。分割行列のメモリサイズは分割数に応じて線形に増加する。従って、メモリ使用量の増加は精度向上の代償となる。
2. 指数範囲の広い入力に対する耐性が弱い。基本的に、要素の指数分布範囲が広い場合、仮数空間全体を保存するために多数の分割が必要となる。

スキームの実際

尾崎らによる別の論文では、DGEMM（倍精度一般行列乗算）をGPU上で実行するためにINT8 TC整数行列乗算ユニットを使用するスキームについて概説している。

この論文では、理論的背景の多くと、下図に示す実際の結果が証明されている。整数INT8テンソルコアを用いた尾崎スキーム（INT8x、Xは分割数）、FP16テンソルコアを用いた同様の尾崎スキーム（椋木らによるozBLAS）、エヌビディア・ライブラリの一部であるcuBLAS DGEMMの結果が含まれている。

テストには4つのGPUが含まれる： エヌビディアA100、TITAN RTX（チューリングアーキテクチャ）、RTX A6000（アンペールアーキテクチャ）、RTX 6000 Ada（エイダ・ラブレスアーキテクチャ）である。

A100では、DGEMMはFP64テンソルコアの理論ピーク性能（19.5TFlop/s）の90%以上のスループットを達成したが、INT8xはDGEMMより3〜5倍遅かった。この結果は、INT8x s 内の整数行列乗算演算数が 45 ∼ 108 であるのに対し、整数テンソルコアの最大性能は FP64 テン ソルコアの最大 20 倍に過ぎないことから予想されるものである（各種 GPU ユニットの性能については上表を参照）。

対照的に、INT8 TCの性能が優れている他のGPUは、エヌビディアDGEMMよりも高速である。この表には、FP16テンソルコアに実装された尾崎スキームも含まれている。すべての場合において、整数テンソルコアの実装はFP16のものよりも高速である。

Int8x13、Int8x11、Int8x9の結果は、性能と精度のトレードオフを明確に示している。この論文では精度についてさらに論じている。

最も顕著なのは、FP64 CUDAコアを使用するエヌビディアDGEMMライブラリに対する性能向上である。さらに、INT8テンソルコアを使用するOzakiスキームは、ワットあたりのパフォーマンスで最高の総合精度レベルを提供する。

スループット（上段）、電力効率（中段）、消費電力（下段）の比較。INT8x（Xは分割数）の実装は整数テンソルコア上の尾崎スキームであり、ozBLASは椋木らによるFP16テンソルコア上の実装であり、cuBLAS DGEMMはエヌビディアCuBLASの一部である。ozBLASの実装では、仮数空間の長さがINT8xと同じになるように分割数を選択し、スライスによって保たれる精度がほぼ同等になるようにしている。(クリックで拡大）

スループット（上段）、電力効率（中段）、消費電力（下段）の比較。INT8x（Xは分割数）の実装は整数テンソルコア上の尾崎スキームであり、ozBLASは椋木らによるFP16テンソルコア上の実装であり、cuBLAS DGEMMはエヌビディアCuBLASの一部である。ozBLAS実装の分割数は、仮数空間長がINT8xと同じになるように選択し、スライスによって保たれる精度はほぼ同等である。

本論文では、ハイパフォーマンスコンピューティング・アプリケーションにおいて、整数行列乗算ユニット（IMMU）上で尾崎スキームを使用することの理論的利点と実用的利点の両方を示す。FP64(64ビット浮動小数点)精度を8ビット整数テンソルコアで維持できる。標準的なFP64 cuBLASライブラリよりも高速であるという事実は非常に注目に値するもので、AIに特化したGPUやアクセラレータ上のHPCアプリケーションにパフォーマンスの道を提供する。

コードが利用可能

Int8テンソルコア上でDGEMMを実行するサンプルコードは、プロジェクトozIMMU（Ozaki-Integer Matrix Multiplication Unit）としてGitHubで公開されている。このライブラリは、cuBLAS DGEMM関数の関数呼び出しをインターセプトし、代わりにozIMMUを実行する。

尾崎スキームについて言及してくれたIntersect 360 Researchのアディソン・スネル氏に感謝する。